Week 4

Effect Decomposition, Random Coefficient Model, and Cross-level Interactions

Week Learning Objectives

By the end of this module, you will be able to

• Explain what the ecological fallacy is
• Use cluster-mean/group-mean centering to decompose the effect of a lv-1 predictor
• Define contextual effects
• Explain the concept of random slopes
• Analyze and interpret cross-level interaction effects

Task Lists

1. Review the resources (lecture videos and slides)
2. Complete the assigned readings
   • Snijders & Bosker ch 4.6, 5.1–5.3
3. Attend the Thursday session and participate in the class exercise
4. Complete Homework 4
5. Now that you have learned the basics of MLM, start thinking about your project (Prospectus due around Oct 18)

Lecture

Slides

You can view and download the slides here: PDF

Overview

Check your learning: The Type I error inflation problem when using OLS regression for clustered data applies to

Level-1 predictors
Level-2 predictors
Level-2 predictors and most level-1 predictors

---

Ecological Fallacy

Check your learning: In a “bizarre” research finding that found a correlation between chocolate consumption and number of Nobel prize winners at the country level, which of the following is reasonable to infer?

That those who eat more chocolate are more likely to win a nobel prize
That nutritional contents in chocolate is related to cognitive functioning
That there are potential third variables that relate to both a country’s chocolate consumption level and the number of Nobel prize winners

Check your learning: Summarize the “Big-Fish-Little-Pond Effect” in terms of how a person’s own academic performance and the overall performance of the person’s school on academic self-concept.

---

Decomposing Effects

Between/within effects

Note: What I called “cluster-mean centering” is the same as “within-group centering” in Snijders & Bosker (2012)

Check your learning: Why do we need to separate a level-1 predictor into two variables in the model?

Because the slope of the level-1 predictor and that of its cluster means may be different
Because there is an interaction between the predictor and the cluster variable
Because the intraclass correlation for any level-1 predictor will be zero

---

Path diagram and equations

Thinking exercise: Based on the between-cluster level component in the path diagram and in the equations, meanses can predict

Both the school-level math achievement and a student’s relative standing within a school
Only a student’s relative standing within a school
Only the school means of math achievement

Check your learning: Based on the results shown in the video, is the school-level slope or the student-level slope larger for the association between SES and math achievement?

School-level
Student-level

---

Interpret the between/within effects

Try it yourself: Obtain the predicted mathach for Student B, and compare with Students A and C.

---

Contextual Effects

Check your learning: The contextual effect is

The predicted difference in the outcome for every unit difference in the cluster mean predictor, holding constant the level-1 predictor
The predicted difference in the outcome for every unit difference in the level-1 predictor, within a given cluster
The between-level effect

---

Random Slopes/Random Coefficients

Developing intuition

Check your learning: In a random-coefficient model, if there are J cluster, there are

one intercept, two slopes
one intercept, J slopes
J intercepts, one slopes
J intercepts, J slopes

---

Equations and path diagram

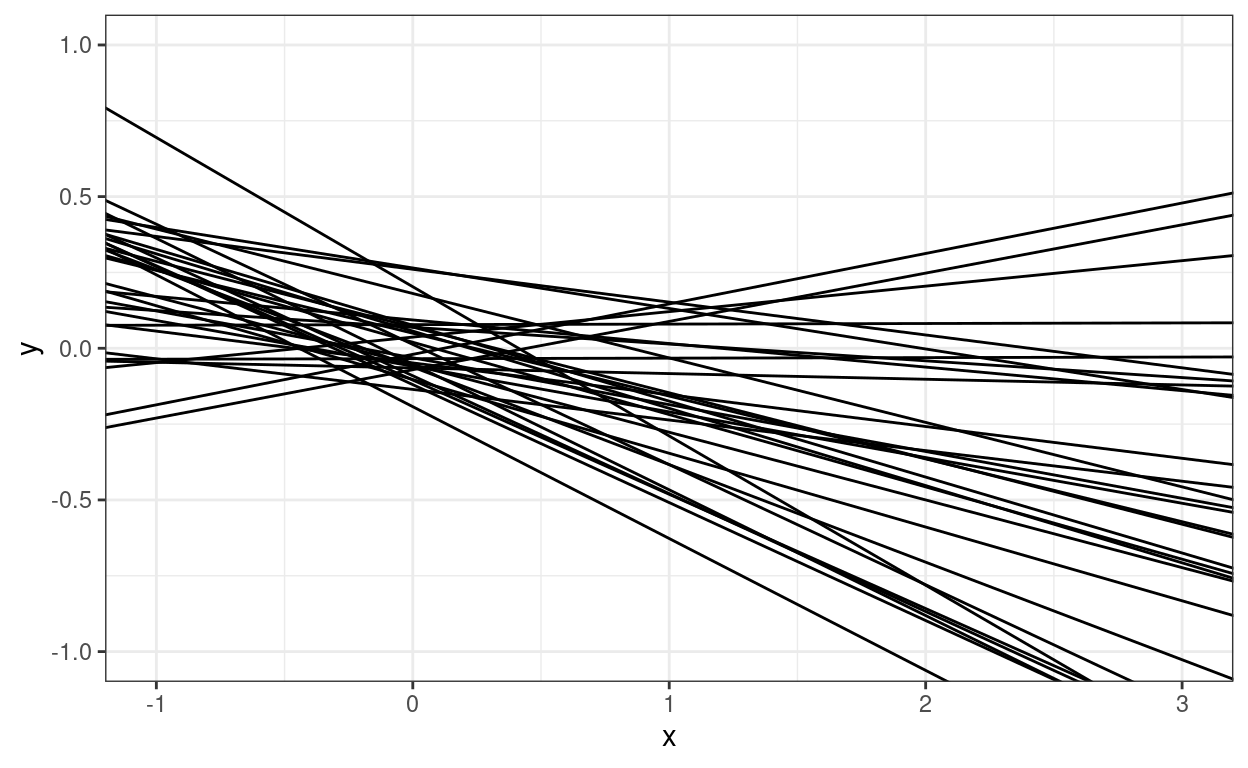
Check your learning: Which combination of τ0 and τ1 best describes the graph below?

tau_0 = 0.1, tau_1 = 0.2
tau_0 = 0, tau_1 = 0.2
tau_0 = 0.1, tau_1 = 0
tau_0 = 0, tau_1 = 0

---

Interpretations

Check your learning: In a random-slope model, if γ10 (the average slope) = 0.2, τ21=0.04, what is the 68% plausible range for the slopes across clusters?

[0, 0.4]
[-0.48, 0.88]
[0.16, 0.24]
[0.12, 0.28]

---

Cross-Level Interaction

In the video, there was a mistake in the path diagram, in that one of the circle should be β1j, not β0j

Check your learning: Conceptually, a cross-level interaction is the same as

An interaction between two level-1 predictors
Using a cluster-level predictor to predict variations in level-1 slopes
Random slopes
Adding the main effect of a cluster-level predictor

---