Click here to download the Rmd file: week4-level-1-predictor.Rmd
Load Packages and Import Data
# To install a package, run the following ONCE (and only once on your computer)
# install.packages("psych")
library(here) # makes reading data more consistent
library(tidyverse) # for data manipulation and plotting
library(haven) # for importing SPSS/SAS/Stata data
library(lme4) # for multilevel analysis
library(sjPlot) # for plotting effects
library(MuMIn) # for computing r-squared
library(broom.mixed) # for summarizing results
library(modelsummary) # for making tables
library(interactions) # for plotting interactions
theme_set(theme_bw()) # Theme; just my personal preference
msummary_mixed <- function(models, coef_map = NULL, ...) {
if (is.null(coef_map)) {
if (!"list" %in% class(models)) {
models <- list(models)
}
for (model in models) {
coef_map <- union(coef_map, tidy(model)$term)
}
ranef_index <- grep("^(sd|cor)__", x = coef_map)
coef_map <- c(coef_map[-ranef_index], coef_map[ranef_index])
names(coef_map) <- coef_map
} else {
ranef_index <- grep("^(sd|cor)__", x = names(coef_map))
}
rows <- data.frame(term = c("Fixed Effects", "Random Effects"))
rows <- cbind(rows, rbind(
rep("", length(models)),
rep("", length(models))
))
length_fes <- length(coef_map) - length(ranef_index)
if ("statistic" %in% names(list(...)) && is.null(list(...)$statistic)) {
attr(rows, "position") <- c(1, (length_fes + 1))
} else {
attr(rows, "position") <- c(1, (length_fes + 1) * 2)
}
modelsummary::msummary(models, coef_map = coef_map, add_rows = rows, ...)
}
Import Data
# Read in the data (pay attention to the directory)
hsball <- read_sav(here("data_files", "hsball.sav"))
Between-Within Decomposition
Cluster-mean centering
To separate the effects of a lv-1 predictor into different levels, one needs to first center the predictor on the cluster means:
hsball <- hsball %>%
group_by(id) %>% # operate within schools
mutate(ses_cm = mean(ses), # create cluster means (the same as `meanses`)
ses_cmc = ses - ses_cm) %>% # cluster-mean centered
ungroup() # exit the "editing within groups" mode
# The meanses variable already exists in the original data, but it's slightly
# different from computing it by hand
hsball %>%
select(id, ses, meanses, ses_cm, ses_cmc)
># # A tibble: 7,185 × 5
># id ses meanses ses_cm ses_cmc
># <chr> <dbl> <dbl> <dbl> <dbl>
># 1 1224 -1.53 -0.428 -0.434 -1.09
># 2 1224 -0.588 -0.428 -0.434 -0.154
># 3 1224 -0.528 -0.428 -0.434 -0.0936
># 4 1224 -0.668 -0.428 -0.434 -0.234
># 5 1224 -0.158 -0.428 -0.434 0.276
># 6 1224 0.022 -0.428 -0.434 0.456
># 7 1224 -0.618 -0.428 -0.434 -0.184
># 8 1224 -0.998 -0.428 -0.434 -0.564
># 9 1224 -0.888 -0.428 -0.434 -0.454
># 10 1224 -0.458 -0.428 -0.434 -0.0236
># # … with 7,175 more rowsModel Equation
Lv-1:
mathachij=β0j+β1jses_cmcij+eij
Lv-2:
β0j=γ00+γ01meansesj+u0jβ1j=γ10
- γ10 = regression
coefficient of student-level
sesrepresenting the expected difference in student achievement between two students in the same school with one unit difference inses,
- γ01 = between-school
effect, which is the expected difference in mean achievement between two
schools with one unit difference in
meanses.
Running in R
We can specify the model as:
m_bw <- lmer(mathach ~ meanses + ses_cmc + (1 | id), data = hsball)
You can summarize the results using
summary(m_bw)
># Linear mixed model fit by REML ['lmerMod']
># Formula: mathach ~ meanses + ses_cmc + (1 | id)
># Data: hsball
>#
># REML criterion at convergence: 46569
>#
># Scaled residuals:
># Min 1Q Median 3Q Max
># -3.167 -0.725 0.017 0.756 2.945
>#
># Random effects:
># Groups Name Variance Std.Dev.
># id (Intercept) 2.69 1.64
># Residual 37.02 6.08
># Number of obs: 7185, groups: id, 160
>#
># Fixed effects:
># Estimate Std. Error t value
># (Intercept) 12.648 0.149 84.7
># meanses 5.866 0.362 16.2
># ses_cmc 2.191 0.109 20.2
>#
># Correlation of Fixed Effects:
># (Intr) meanss
># meanses -0.004
># ses_cmc 0.000 0.000Contextual Effect
With a level-1 predictor like ses, which has both
student-level and school-level variance, we can include both the level-1
variable and the school mean variable as predictors. When the level-1
predictor is present, the coefficient for the group mean variable
becomes the contextual effect.
Model Equation
Lv-1:
mathachij=β0j+β1jsesij+eij
Lv-2:
β0j=γ00+γ01meansesj+u0jβ1j=γ10
- γ10 = regression
coefficient of student-level
sesrepresenting the expected difference in student achievement between two students in the same school with one unit difference inses,
- γ01 = contextual
effect, which is the expected difference in student achievement between
two students with the same
sesbut from two schools with one unit difference inmeanses.
Running in R
We can specify the model as:
contextual <- lmer(mathach ~ meanses + ses + (1 | id), data = hsball)
You can summarize the results using
summary(contextual)
># Linear mixed model fit by REML ['lmerMod']
># Formula: mathach ~ meanses + ses + (1 | id)
># Data: hsball
>#
># REML criterion at convergence: 46569
>#
># Scaled residuals:
># Min 1Q Median 3Q Max
># -3.167 -0.725 0.017 0.756 2.945
>#
># Random effects:
># Groups Name Variance Std.Dev.
># id (Intercept) 2.69 1.64
># Residual 37.02 6.08
># Number of obs: 7185, groups: id, 160
>#
># Fixed effects:
># Estimate Std. Error t value
># (Intercept) 12.661 0.149 84.76
># meanses 3.675 0.378 9.73
># ses 2.191 0.109 20.16
>#
># Correlation of Fixed Effects:
># (Intr) meanss
># meanses -0.005
># ses 0.004 -0.288If you compare the REML criterion at convergence number
you can see this is the same as the between-within model. The estimated
contextual effect is the coefficient of meanses minus the
coefficient of ses_cmc, which is the same as what you will
get in the contextual effect model.
Random-Coefficients Model
Explore Variations in Slopes
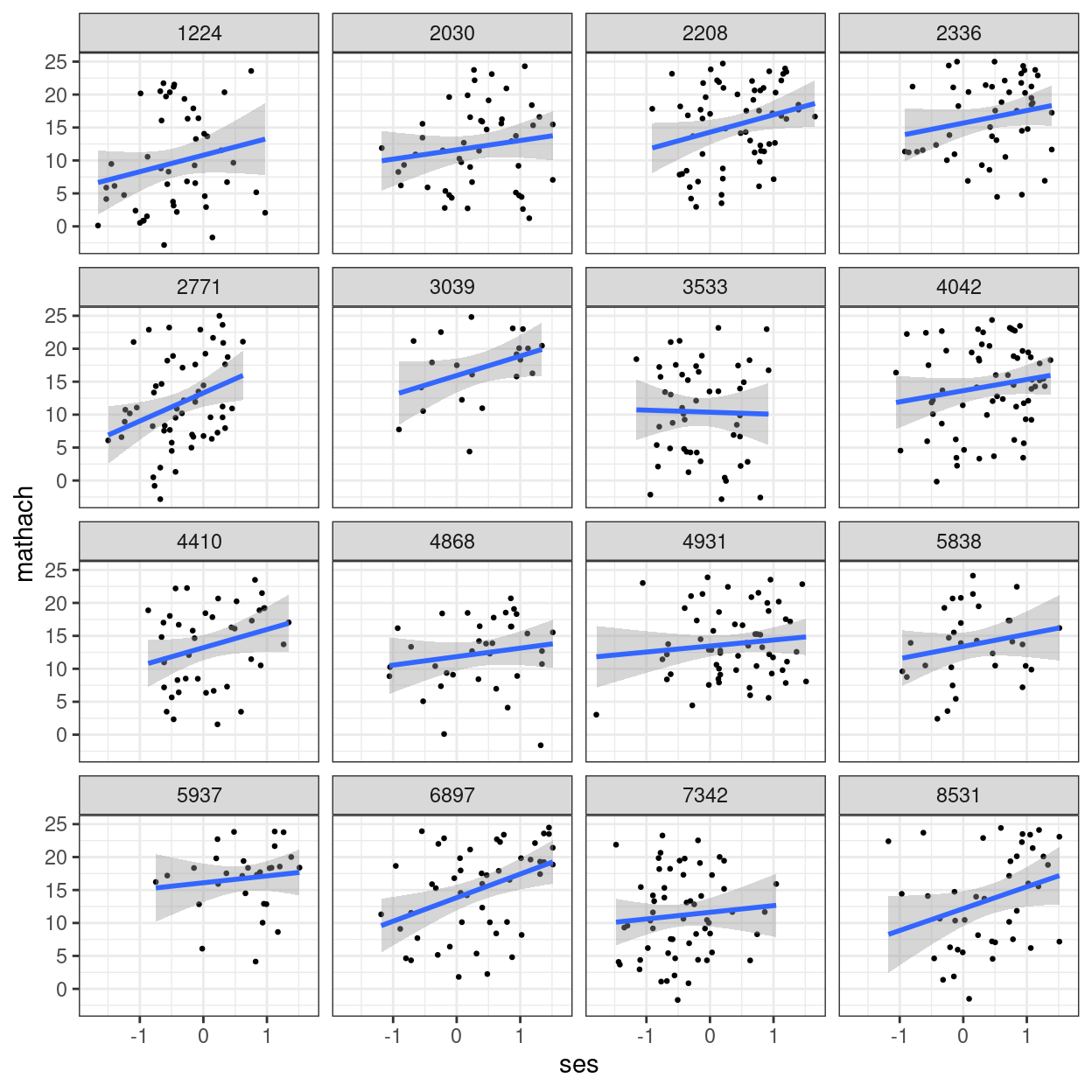
hsball %>%
# randomly sample 16 schools
filter(id %in% sample(unique(id), 16)) %>%
ggplot(aes(x = ses, y = mathach)) +
geom_point(size = 0.5) +
geom_smooth(method = "lm") +
facet_wrap(~id)
Model Equation
Lv-1:
mathachij=β0j+β1jses_cmcij+eij
Lv-2:
β0j=γ00+γ01meansesj+u0jβ1j=γ10+u1j
Running in R
We have to put ses in the random part:
ran_slp <- lmer(mathach ~ meanses + ses_cmc + (ses_cmc | id), data = hsball)
You can summarize the results using
summary(ran_slp)
># Linear mixed model fit by REML ['lmerMod']
># Formula: mathach ~ meanses + ses_cmc + (ses_cmc | id)
># Data: hsball
>#
># REML criterion at convergence: 46558
>#
># Scaled residuals:
># Min 1Q Median 3Q Max
># -3.177 -0.727 0.016 0.756 2.941
>#
># Random effects:
># Groups Name Variance Std.Dev. Corr
># id (Intercept) 2.693 1.641
># ses_cmc 0.686 0.828 -0.19
># Residual 36.713 6.059
># Number of obs: 7185, groups: id, 160
>#
># Fixed effects:
># Estimate Std. Error t value
># (Intercept) 12.645 0.149 84.7
># meanses 5.896 0.360 16.4
># ses_cmc 2.191 0.128 17.1
>#
># Correlation of Fixed Effects:
># (Intr) meanss
># meanses -0.004
># ses_cmc -0.088 0.004Plotting Random Slopes
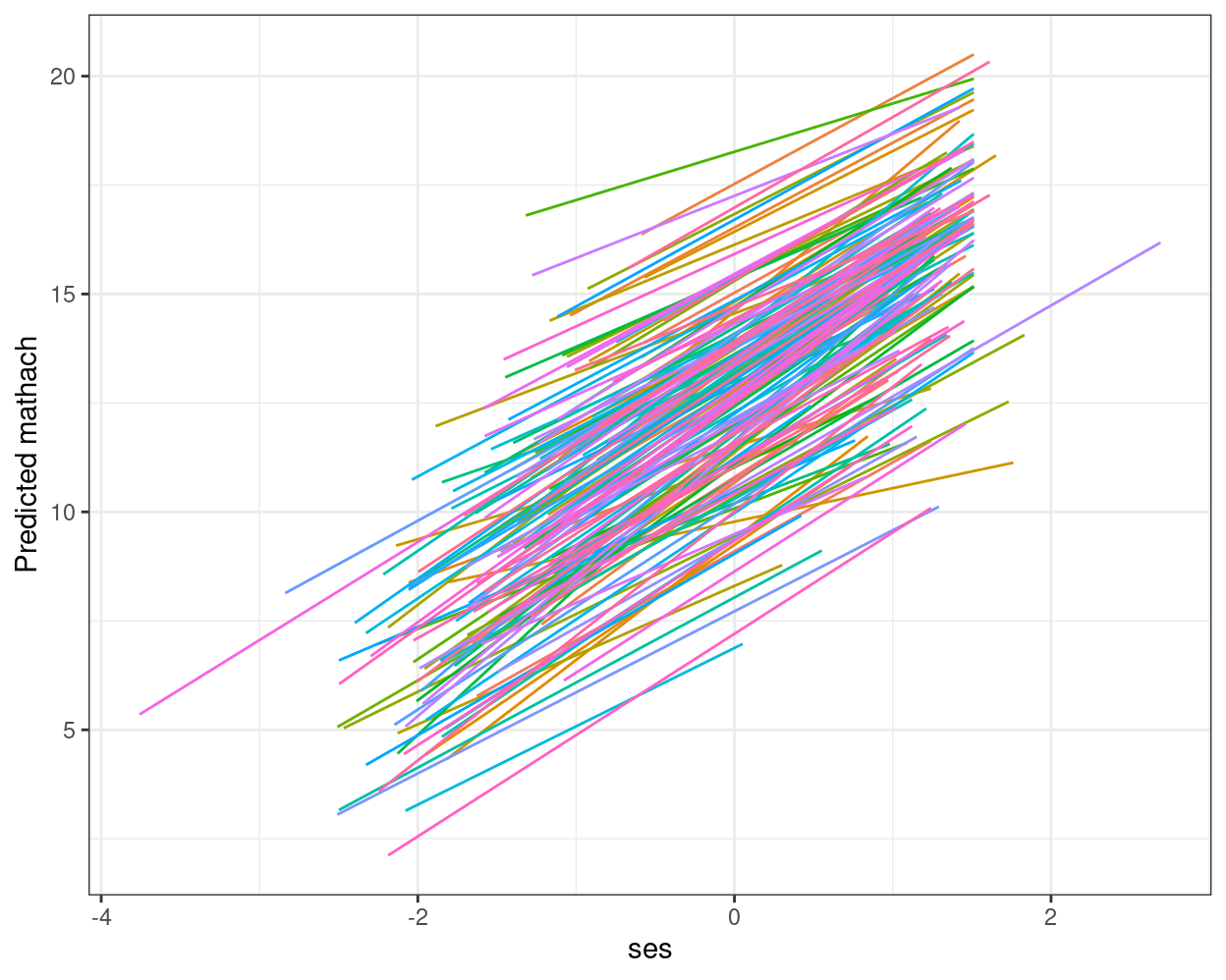
augment(ran_slp, data = hsball) %>% # augmented data (adding EB estimates)
ggplot(aes(x = ses, y = .fitted, color = factor(id))) +
geom_smooth(method = "lm", se = FALSE, size = 0.5) +
labs(y = "Predicted mathach") +
guides(color = "none")
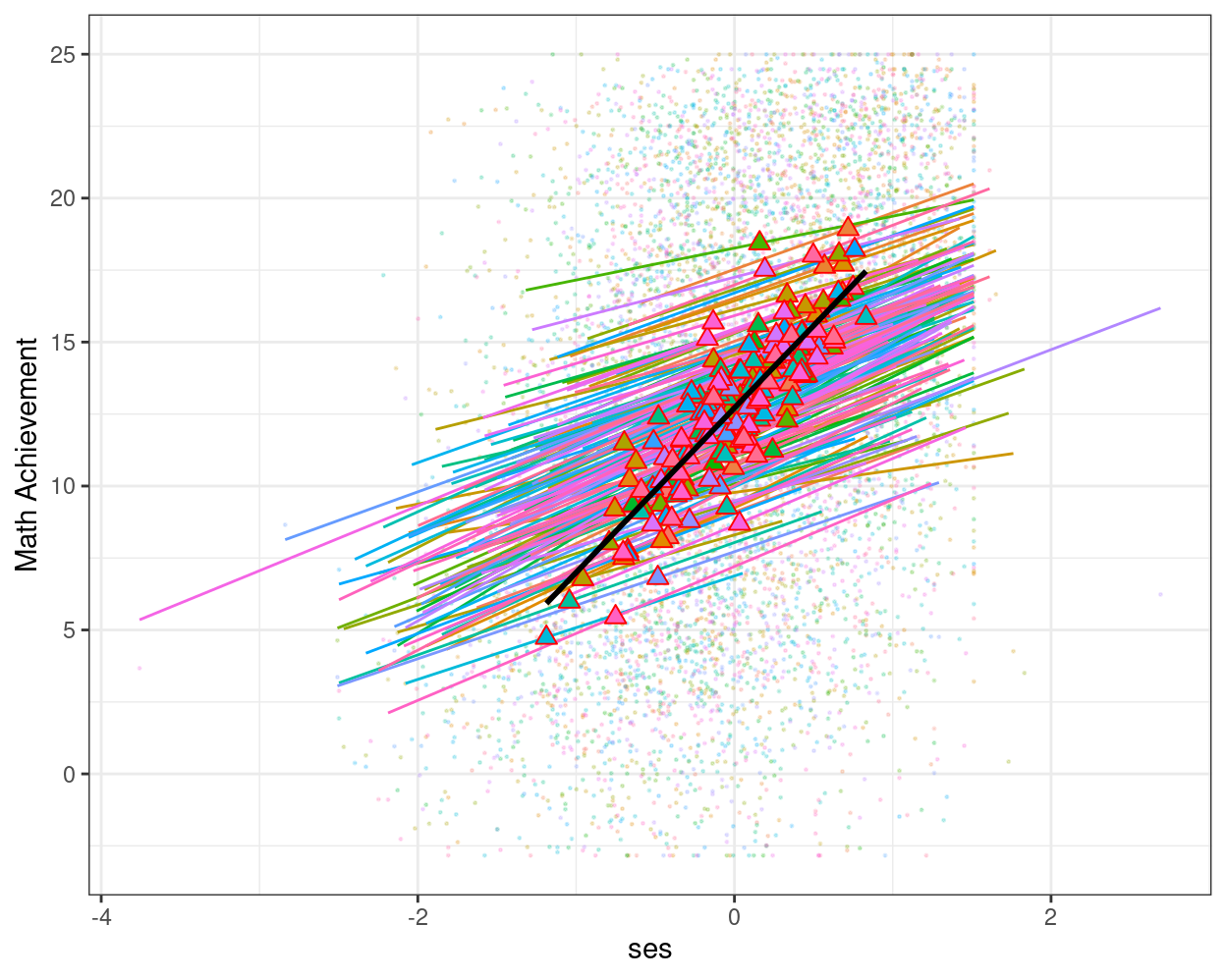
Including the effect of
meanses
# augmented data (adding EB estimates)
augment(ran_slp, data = hsball) %>%
ggplot(aes(x = ses, y = mathach, color = factor(id))) +
# Add points
geom_point(size = 0.2, alpha = 0.2) +
# Add within-cluster lines
geom_smooth(aes(y = .fitted),
method = "lm", se = FALSE, size = 0.5) +
# Add group means
stat_summary(aes(x = meanses, y = .fitted,
fill = factor(id)),
color = "red", # add border
fun = mean,
geom = "point",
shape = 24,
# use triangles
size = 2.5) +
# Add between coefficient
geom_smooth(aes(x = meanses, y = .fitted),
method = "lm", se = FALSE,
color = "black") +
labs(y = "Math Achievement") +
# Suppress legend
guides(color = "none", fill = "none")
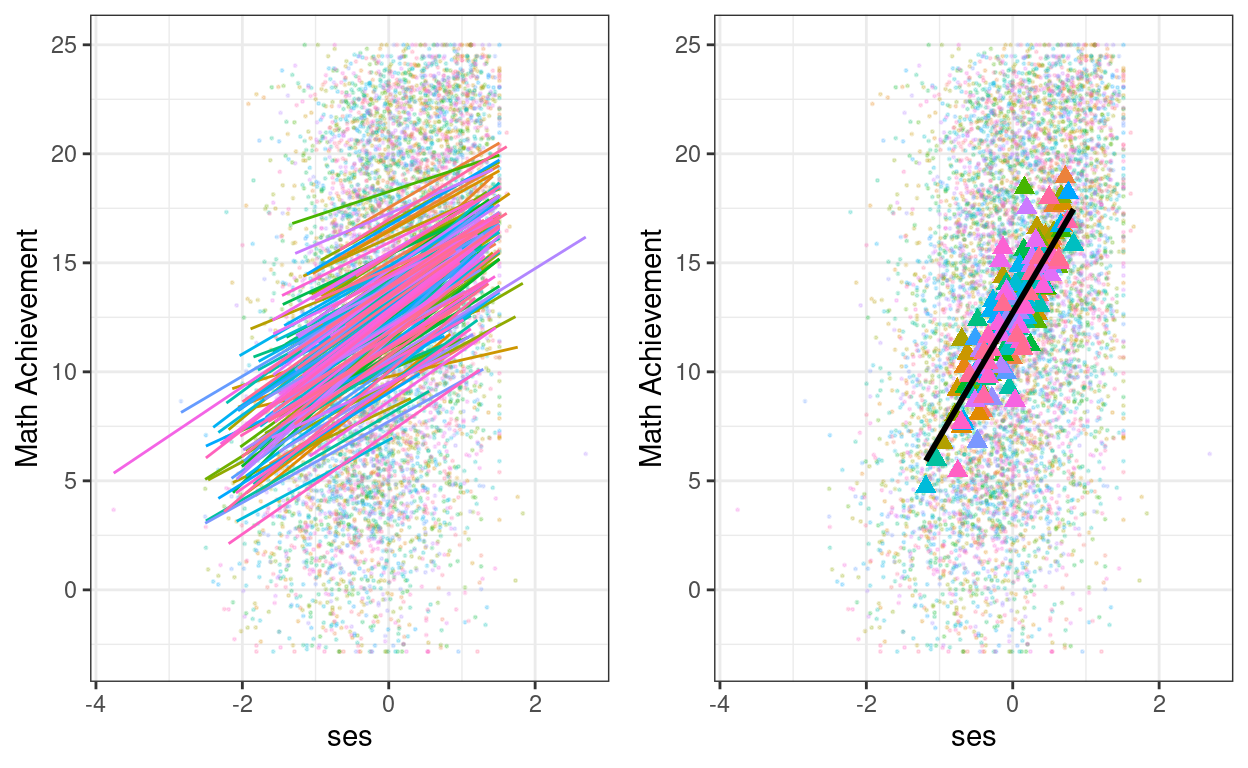
Or on separate graphs:
# Create a common base graph
pbase <- augment(ran_slp, data = hsball) %>%
ggplot(aes(x = ses, y = mathach, color = factor(id))) +
# Add points
geom_point(size = 0.2, alpha = 0.2) +
labs(y = "Math Achievement") +
# Suppress legend
guides(color = "none")
# Lv-1 effect
p1 <- pbase +
# Add within-cluster lines
geom_smooth(aes(y = .fitted),
method = "lm", se = FALSE, size = 0.5)
# Lv-2 effect
p2 <- pbase +
# Add group means
stat_summary(aes(x = meanses, y = .fitted),
fun = mean,
geom = "point",
shape = 17,
# use triangles
size = 2.5) +
# Add between coefficient
geom_smooth(aes(x = meanses, y = .fitted),
method = "lm", se = FALSE,
color = "black")
# Put the two graphs together (need the gridExtra package)
gridExtra::grid.arrange(p1, p2, ncol = 2) # in two columns
Effect Size
As discussed in the previous week, we can obtain the effect size (R2) for the model:
(r2_ran_slp <- r.squaredGLMM(ran_slp))
># R2m R2c
># [1,] 0.1684 0.2311Analyzing Cross-Level Interactions
sector is added to the level-2 intercept and slope
equations
Model Equation
Lv-1:
mathachij=β0j+β1jses_cmcij+eij
Lv-2:
β0j=γ00+γ01meansesj+γ02sectorj+u0jβ1j=γ10+γ11sectorj+u1jsector variable
representing the expected difference in achievement between two students
with the same SES level and from two schools with the same school-level
SES, but one is a catholic school and the other a private school. -
γ11 = cross-level
interaction coefficient of the expected slope difference
between a catholic and a private school with the same school-level
SES.
Running in R
We have to put the sector * ses interaction to the fixed
part:
# The first step is optional, but let's recode sector into a factor variable
hsball <- hsball %>%
mutate(sector = factor(sector, levels = c(0, 1),
labels = c("Public", "Catholic")))
crlv_int <- lmer(mathach ~ meanses + sector * ses_cmc + (ses_cmc | id),
data = hsball)
You can summarize the results using
summary(crlv_int)
># Linear mixed model fit by REML ['lmerMod']
># Formula: mathach ~ meanses + sector * ses_cmc + (ses_cmc | id)
># Data: hsball
>#
># REML criterion at convergence: 46514
>#
># Scaled residuals:
># Min 1Q Median 3Q Max
># -3.1156 -0.7291 0.0159 0.7528 3.0154
>#
># Random effects:
># Groups Name Variance Std.Dev. Corr
># id (Intercept) 2.381 1.543
># ses_cmc 0.272 0.521 0.24
># Residual 36.708 6.059
># Number of obs: 7185, groups: id, 160
>#
># Fixed effects:
># Estimate Std. Error t value
># (Intercept) 12.085 0.199 60.81
># meanses 5.245 0.368 14.24
># sectorCatholic 1.252 0.306 4.09
># ses_cmc 2.788 0.156 17.89
># sectorCatholic:ses_cmc -1.348 0.235 -5.74
>#
># Correlation of Fixed Effects:
># (Intr) meanss sctrCt ss_cmc
># meanses 0.245
># sectorCthlc -0.697 -0.355
># ses_cmc 0.071 -0.002 -0.046
># sctrCthlc:_ -0.048 -0.001 0.071 -0.664Effect Size
By comparing the R2 of this model (with interaction) and the previous model (without the interaction), we can obtain the proportion of variance accounted for by the cross-level interaction:
(r2_crlv_int <- r.squaredGLMM(crlv_int))
># R2m R2c
># [1,] 0.1759 0.2284# Change
r2_crlv_int - r2_ran_slp
># R2m R2c
># [1,] 0.007496 -0.002643Therefore, the cross-level interaction between sector and SES accounted for an effect size of ΔR2 = 0.7%. This is usually considered a small effect size (i.e., < 1%), but interpreting the magnitude of an effect size needs to take into account the area of research, the importance of the outcome, and the effect sizes when using other predictors to predict the same outcome.
Simple Slopes
With a cross-level interaction, the slope between
ses_cmc and mathach depends on a moderator,
sector. To find out what the model suggests to be the slope
at a particular level of sector, which is also called a
simple slope in the literature, you just need to look at the
equation for β1j, which
shows that the predicted slope is ˆβ1=ˆγ10+ˆγ11sector.sector = 0 (public school), the simple slope is
ˆβ1=ˆγ10+ˆγ11(0),sector = 1
(private school), the simple slope is ˆβ1=ˆγ10+ˆγ11(1),
Plotting the Interactions
crlv_int %>%
augment(data = hsball) %>%
ggplot(aes(
x = ses, y = .fitted, group = factor(id),
color = factor(sector) # use `sector` for coloring lines
)) +
geom_smooth(method = "lm", se = FALSE, size = 0.5) +
labs(y = "Predicted mathach", color = "sector")
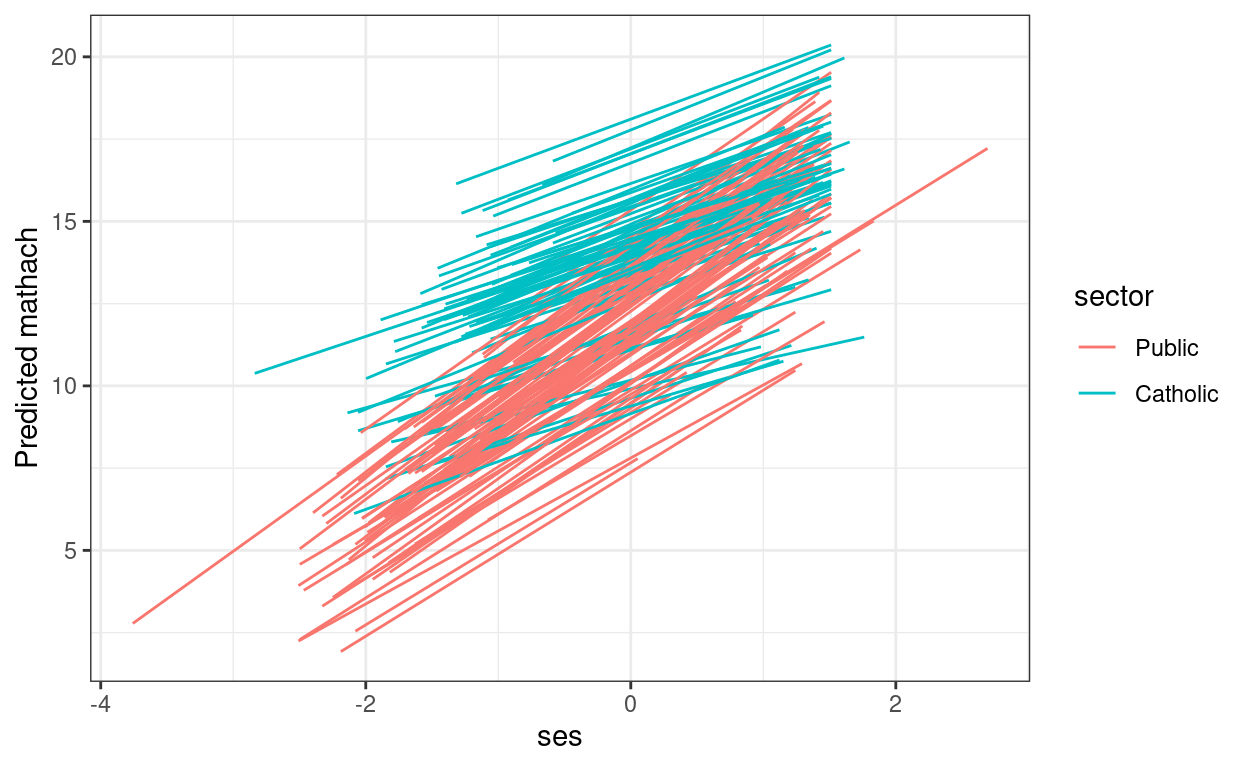
You can also use the interactions::interact_plot()
function for just the fixed effects:
interact_plot(crlv_int,
pred = "ses_cmc",
modx = "sector",
modx.labels = c("Public", "Catholic"),
plot.points = TRUE,
point.size = 0.5,
point.alpha = 0.2,
facet.modx = TRUE, # use this to make two panels
x.label = "SES (cluster-mean centered)",
y.label = "Math achievement")
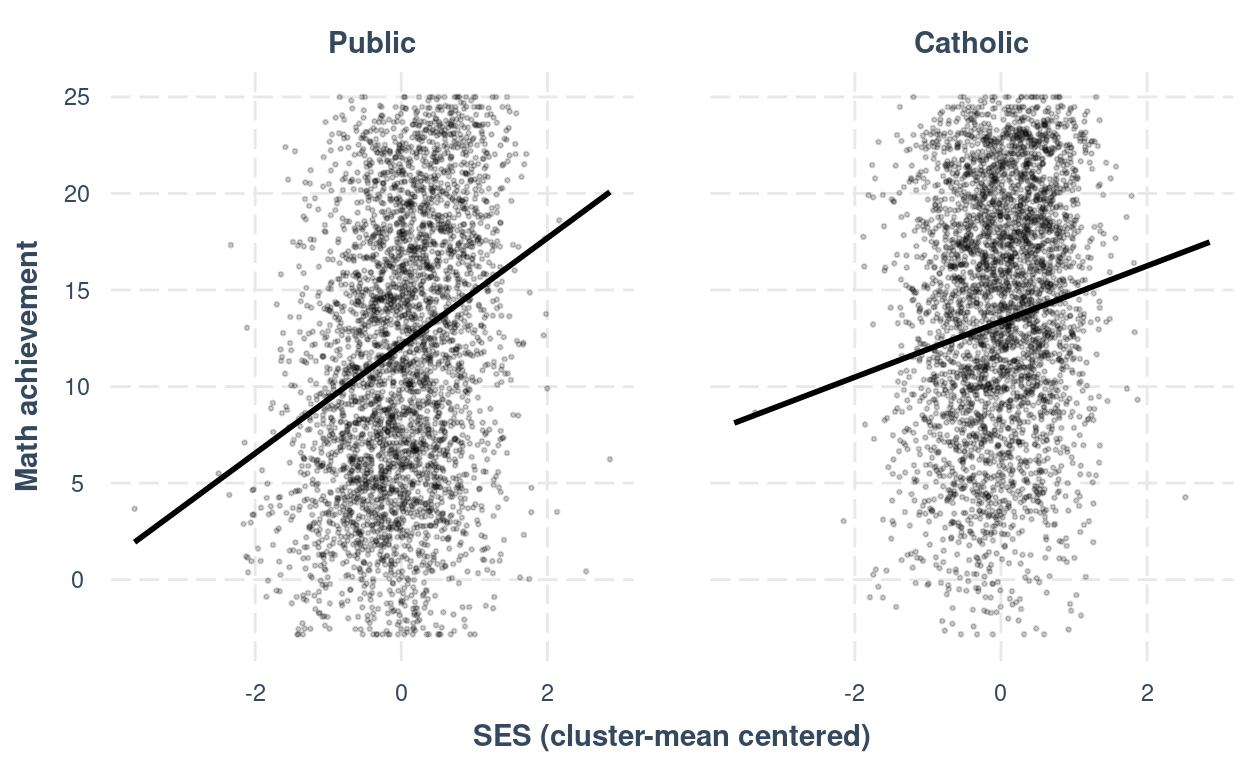
Summaizing Analyses in a Table
You can again use the msummary() function from the
modelsummary package to quickly summarize the results in a
table. However, there is an issue as the order of the coefficients are
messed up, as shown below.
# Basic table from `modelsummary` (ordering messed up)
msummary(list(
"Between-within" = m_bw,
"Contextual" = contextual,
"Random slope" = ran_slp,
"Cross-level interaction" = crlv_int
))
| Between-within | Contextual | Random slope | Cross-level interaction | |
|---|---|---|---|---|
| (Intercept) | 12.648 | 12.661 | 12.645 | 12.085 |
| (0.149) | (0.149) | (0.149) | (0.199) | |
| meanses | 5.866 | 3.675 | 5.896 | 5.245 |
| (0.362) | (0.378) | (0.360) | (0.368) | |
| ses_cmc | 2.191 | 2.191 | 2.788 | |
| (0.109) | (0.128) | (0.156) | ||
| sd__(Intercept) | 1.641 | 1.641 | 1.641 | 1.543 |
| sd__Observation | 6.084 | 6.084 | 6.059 | 6.059 |
| ses | 2.191 | |||
| (0.109) | ||||
| cor__(Intercept).ses_cmc | −0.195 | 0.244 | ||
| sd__ses_cmc | 0.828 | 0.521 | ||
| sectorCatholic | 1.252 | |||
| (0.306) | ||||
| sectorCatholic × ses_cmc | −1.348 | |||
| (0.235) | ||||
| Num.Obs. | 7185 | 7185 | 7185 | 7185 |
| AIC | 46578.6 | 46578.6 | 46571.7 | 46532.5 |
| BIC | 46613.0 | 46613.0 | 46619.8 | 46594.4 |
| Log.Lik. | −23284.289 | −23284.290 | −23278.825 | −23257.264 |
| REMLcrit | 46568.577 | 46568.580 | 46557.651 | 46514.529 |
I’ve made a function msummary_mixed(), defined in the
beginning of this page, as a hack to get a nicer table. Basically, you
can just replace msummary() with
msummary_mixed(), with everything else being the same:
# Basic table using `msummary_mixed`
msummary_mixed(list(
"Between-within" = m_bw,
"Contextual" = contextual,
"Random slope" = ran_slp,
"Cross-level interaction" = crlv_int
))
| Between-within | Contextual | Random slope | Cross-level interaction | |
|---|---|---|---|---|
| Fixed Effects | ||||
| (Intercept) | 12.648 | 12.661 | 12.645 | 12.085 |
| (0.149) | (0.149) | (0.149) | (0.199) | |
| meanses | 5.866 | 3.675 | 5.896 | 5.245 |
| (0.362) | (0.378) | (0.360) | (0.368) | |
| ses_cmc | 2.191 | 2.191 | 2.788 | |
| (0.109) | (0.128) | (0.156) | ||
| ses | 2.191 | |||
| (0.109) | ||||
| sectorCatholic | 1.252 | |||
| (0.306) | ||||
| sectorCatholic:ses_cmc | −1.348 | |||
| (0.235) | ||||
| Random Effects | ||||
| sd__(Intercept) | 1.641 | 1.641 | 1.641 | 1.543 |
| sd__Observation | 6.084 | 6.084 | 6.059 | 6.059 |
| cor__(Intercept).ses_cmc | −0.195 | 0.244 | ||
| sd__ses_cmc | 0.828 | 0.521 | ||
| Num.Obs. | 7185 | 7185 | 7185 | 7185 |
| AIC | 46578.6 | 46578.6 | 46571.7 | 46532.5 |
| BIC | 46613.0 | 46613.0 | 46619.8 | 46594.4 |
| Log.Lik. | −23284.289 | −23284.290 | −23278.825 | −23257.264 |
| REMLcrit | 46568.577 | 46568.580 | 46557.651 | 46514.529 |
Bonus: More “APA-like” Table
Make it look like the table at https://apastyle.apa.org/style-grammar-guidelines/tables-figures/sample-tables#regression. You can see a recent recommendation in this paper published in the Journal of Memory and Language
# Step 1. Create a map for the predictors and the terms in the model.
# Need to use '\\( \\)' to show math.
# Rename and reorder the rows. Need to use '\\( \\)' to
# show math. If this does not work for you, don't worry about it.
cm <- c("(Intercept)" = "Intercept",
"meanses" = "school mean SES",
"ses_cmc" = "SES (cluster-mean centered)",
"sectorCatholic" = "Catholic school",
"sectorCatholic:ses_cmc" = "Catholic school x SES (cmc)",
"sd__(Intercept)" = "\\(\\tau_0\\)",
"sd__ses_cmc" = "\\(\\tau_1\\) (SES)",
"sd__Observation" = "\\(\\sigma\\)")
# Step 2. Create a list of models to have one column for coef,
# one for SE, one for CI, and one for p
models <- list(
"Estimate" = crlv_int,
"SE" = crlv_int,
"95% CI" = crlv_int
)
# Step 3. Add rows to say fixed and random effects
# (Need same number of columns as the table)
new_rows <- data.frame(
term = c("Fixed effects", "Random effects"),
est = c("", ""),
se = c("", ""),
ci = c("", "")
)
# Specify which rows to add
attr(new_rows, "position") <- c(1, 7)
# Step 4. Render the table
msummary(models,
estimate = c("estimate", "std.error",
"[{conf.low}, {conf.high}]"),
statistic = NULL, # suppress the extra rows for SEs
coef_map = cm,
add_rows = new_rows)
| Estimate | SE | 95% CI | |
|---|---|---|---|
| Fixed effects | |||
| Intercept | 12.085 | 0.199 | [11.695, 12.474] |
| school mean SES | 5.245 | 0.368 | [4.523, 5.967] |
| SES (cluster-mean centered) | 2.788 | 0.156 | [2.482, 3.093] |
| Catholic school | 1.252 | 0.306 | [0.652, 1.852] |
| Catholic school x SES (cmc) | −1.348 | 0.235 | [−1.808, −0.888] |
| Random effects | |||
| τ0 | 1.543 | ||
| τ1 (SES) | 0.521 | ||
| σ | 6.059 | ||
| Num.Obs. | 7185 | 7185 | 7185 |
| AIC | 46532.5 | 46532.5 | 46532.5 |
| BIC | 46594.4 | 46594.4 | 46594.4 |
| Log.Lik. | −23257.264 | −23257.264 | −23257.264 |
| REMLcrit | 46514.529 | 46514.529 | 46514.529 |