Sample Size Planning for MLM
PSYC 575
Winnie Tse, Mark Lai
University of Southern California
Updated: 2021-11-13
Week Learning Objectives
Describe the importance of having sufficient sample size for scientific research
Describe conceptually the steps for sample size planning: precision analysis and power analysis
Perform power analysis for MLM using the PowerUpR application and the
simrpackageUnderstand the effect of uncertainty in parameter values and explore alternative approaches for sample size planning
Why Sample Size?
Small Sample Size is a Problem Because . . .
Low power
Misleading and noisy results1
- When coupled with publication bias (statistical significance filter)2 3
Nonreproducible findings
Review: Sampling distributions
Test yourself! -- Week 13 Quiz (ungraded)
What is the null distribution?
- Suppose we examine the effect of a therapy on eating disorder
- We test against the null hypothesis H0:γ01=0, where γ01 is the fixed effect of the therapy on eating disorder
What is the alternative distribution?
- Assume that the true effect of this therapy is γ01=.1
Sampling Distribution as a Function of Sample Size
Assume true effect is γ01=0.10
Let's say
- when N=20, p<.05 when ^γ≥0.82
- when N=200, p<.05 when ^γ≥0.26
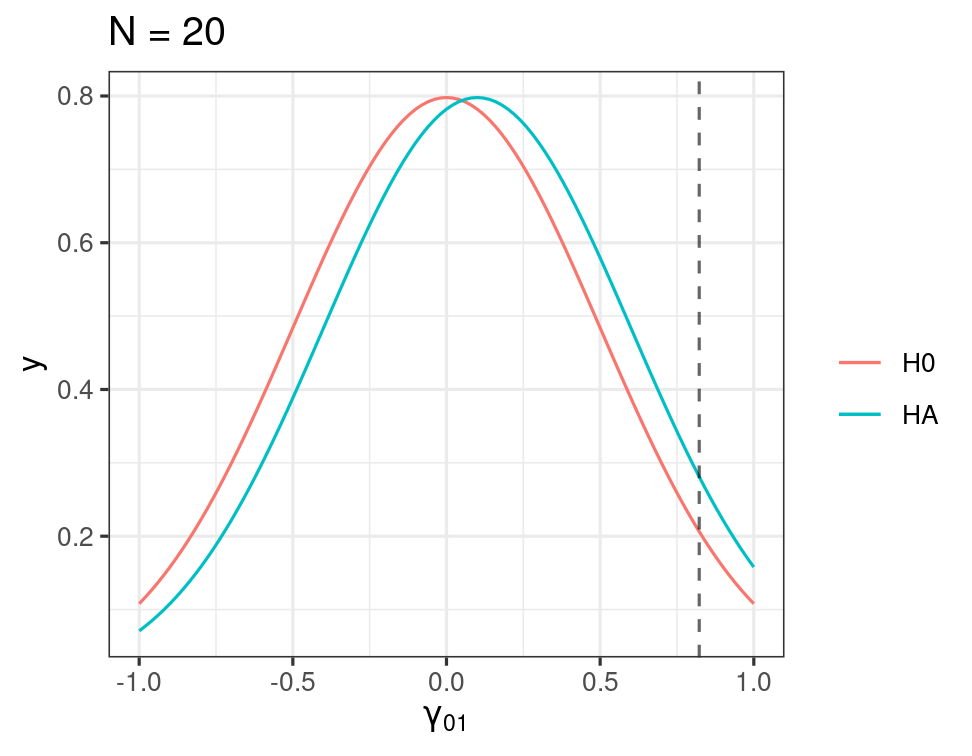

Add the 0 line, the 0.1 line, and the cutoff lines
Steps for Sample Size Planning
Steps for Sample Size Planning
Write down your model equations
List out all parameters in the model
Determine if you want to achieve a desired level of
a. Power, or
b. Precision
Step 1: Write down model equations
Group-based therapy for eating disorder (cluster-randomized trial)
Step 1: Write down model equations
Group-based therapy for eating disorder (cluster-randomized trial)
Level-1 Yij=β0j+β1jX_cmcij+eij eij∼N(0,σ) Level-2 β0j=γ00+γ01Wj+u0jβ1j=γ10+γ11Wj+u1j[u0ju1j]∼N([00],[τ20τ01τ21])
Step 1: Write down model equations
Group-based therapy for eating disorder (cluster-randomized trial)
Level-1 Yij=β0j+β1jX_cmcij+eij eij∼N(0,σ) Level-2 β0j=γ00+γ01Wj+u0jβ1j=γ10+γ11Wj+u1j[u0ju1j]∼N([00],[τ20τ01τ21])
- γ10: X (purely level-1 with ICC = 0)
- γ01: W (level-2)
- γ11: W×X (cross-level interaction)
Step 2: List out all parameters
Fixed effects: γ00, γ01, γ10, γ11
Random effects: τ20, τ21, τ01
Number of clusters: J
Cluster size: n
Level-1 Yij=β0j+β1jX_cmcij+eij eij∼N(0,σ) Level-2 β0j=γ00+γ01Wj+u0jβ1j=γ10+γ11Wj+u1j[u0ju1j]∼N([00],[τ20τ01τ21])
Standard Error and Precision Analysis
Sample Size and SE/Post. SD
In the previous graph, when N=20, the sample estimate is likely to be anywhere between -0.4 and 0.6
SE∝1√N
Sample Size and SE/Post. SD
In the previous graph, when N=20, the sample estimate is likely to be anywhere between -0.4 and 0.6
SE∝1√N
One goal of sample size planning is to
Have sufficient sample size to get precise (low SE) sample estimates of an effect
Analytic Formulas of SE
J = Number of clusters; n = Cluster size
- E.g., J=100 schools; n=10 students per school
Assuming τ01=0
SE(γ01)= ⎷1S2W(τ20J+σ2Jn)SE(γ10)= ⎷τ21J+σ2JnS2XSE(γ11)= ⎷1S2W(τ21J+σ2JnS2X)
Precision Analysis
Group-based therapy for eating disorder (cluster-randomized trial)
Intervention at group level
10 participants per group
Outcome standardized (i.e., SD = √τ20+σ2=1)
- γ = Cohen's d
ICC = .3 (i.e., τ20=.3)
Precision Analysis
Group-based therapy for eating disorder (cluster-randomized trial)
Intervention at group level
10 participants per group
Outcome standardized (i.e., SD = √τ20+σ2=1)
- γ = Cohen's d
ICC = .3 (i.e., τ20=.3)
Goal: estimate J such that SE(γ10)≤.1
- E.g., if we estimated the sample effect size to be d=.25, the 95% CI would be approximately [.05, .45].
Calculating J
When the predictor is binary (e.g., treatment-control), if half of the groups is in one condition, S2W=0.25
- Otherwise, if 30% in one condition, S2W=0.3×0.7
- τ20=0.3, σ2=0.7, n=10
E.g., if J=30 SE(γ01)= ⎷1S2W(τ20J+σ2Jn)=√10.25(0.330+0.7(30)(10))=0.2221111
Calculating J
When the predictor is binary (e.g., treatment-control), if half of the groups is in one condition, S2W=0.25
- Otherwise, if 30% in one condition, S2W=0.3×0.7
- τ20=0.3, σ2=0.7, n=10
E.g., if J=30 SE(γ01)= ⎷1S2W(τ20J+σ2Jn)=√10.25(0.330+0.7(30)(10))=0.2221111
Keep trying, and you'll find ...
When J = 148, SE(γ01)=0.1
So you'll need 148 groups (74 treatment, 74 control)
Power Analysis
Two-tailed test, α=.05
H0:γ01=0
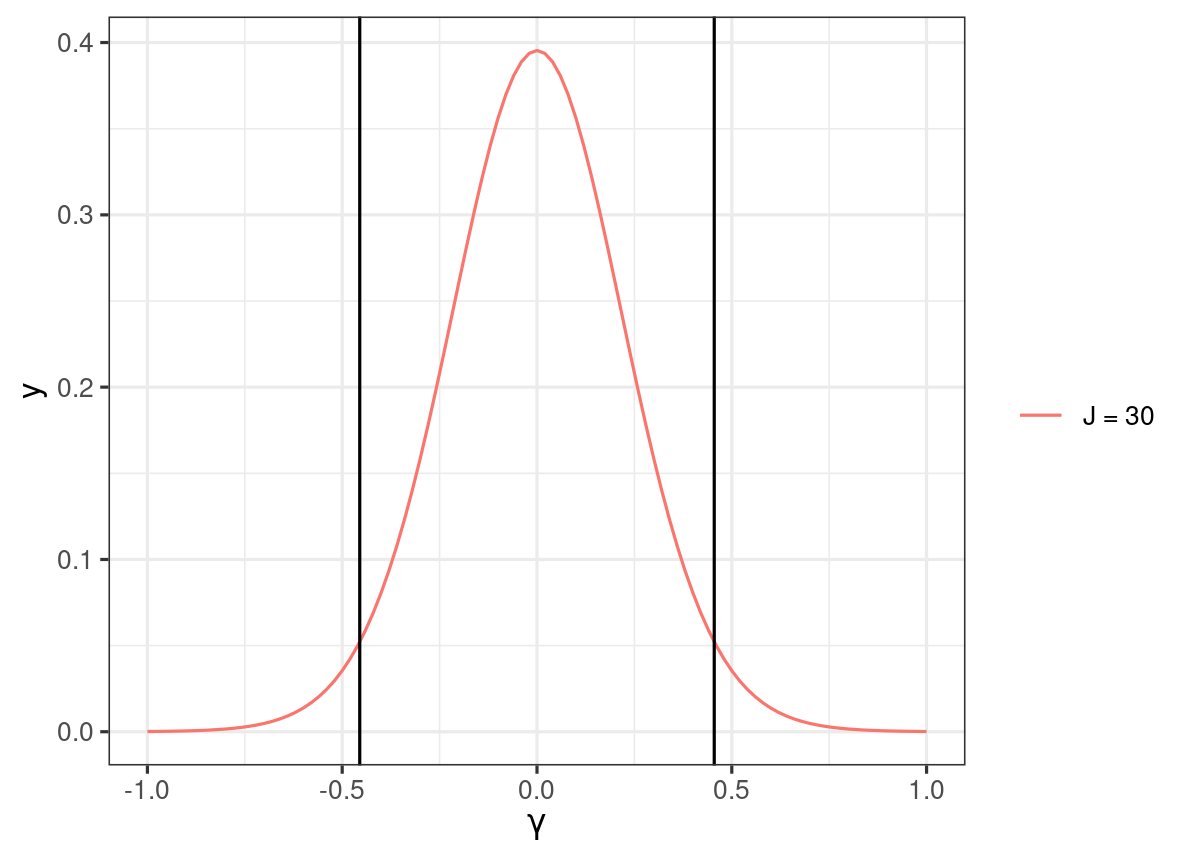
Critical region: ^γ01≤−0.45 or ^γ01≥0.45
Two-tailed test, α=.05
H0:γ01=0

Critical region: ^γ01≤−0.45 or ^γ01≥0.45
H1:γ01=0.3
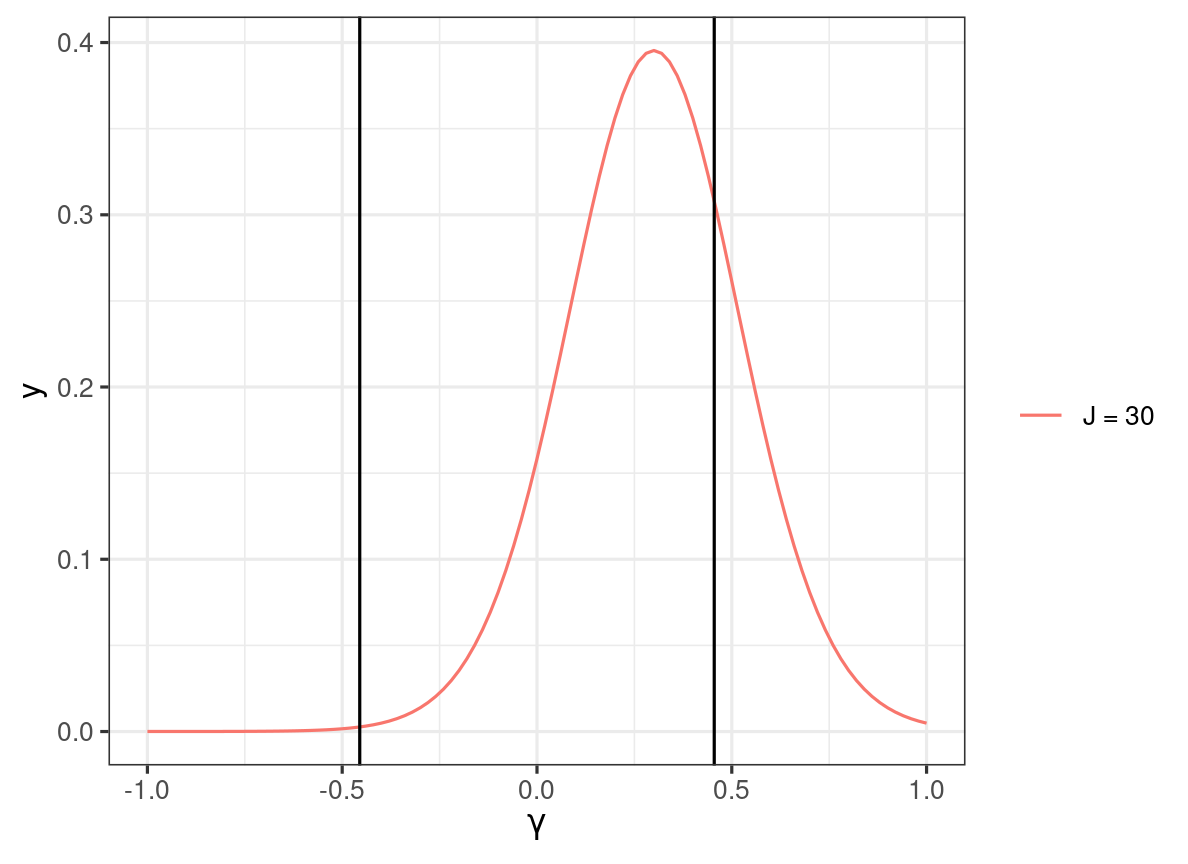
Power1 ≈P(^γ01≤−0.45)+P(^γ01≥0.45)=0.2465731
[1] In practice, we need to incorporate the sampling variability of the standard error as well, so this power calculation is only a rough approximation.
Two-tailed test, α=.05
H0:γ01=0
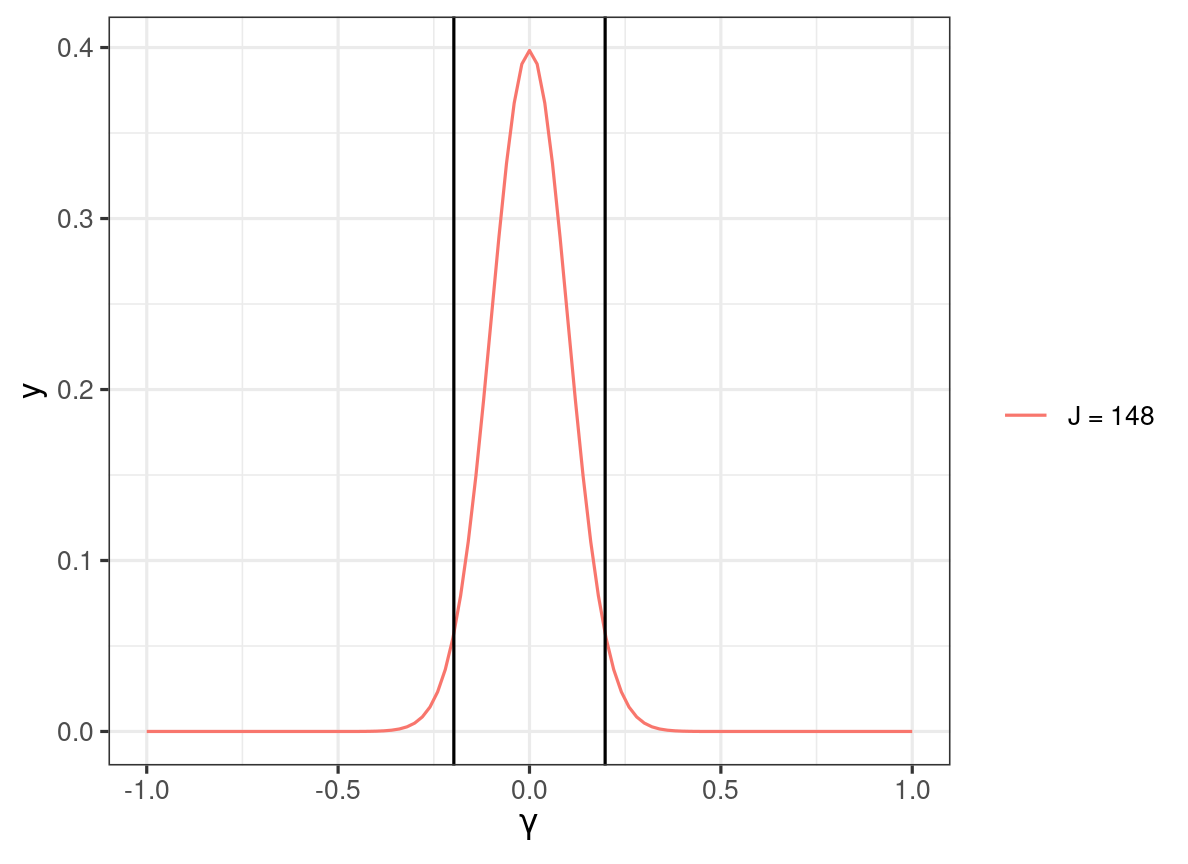
Critical region: ^γ01≤−0.2 or ^γ01≥0.2
Two-tailed test, α=.05
H0:γ01=0

Critical region: ^γ01≤−0.2 or ^γ01≥0.2
H1:γ01=0.3
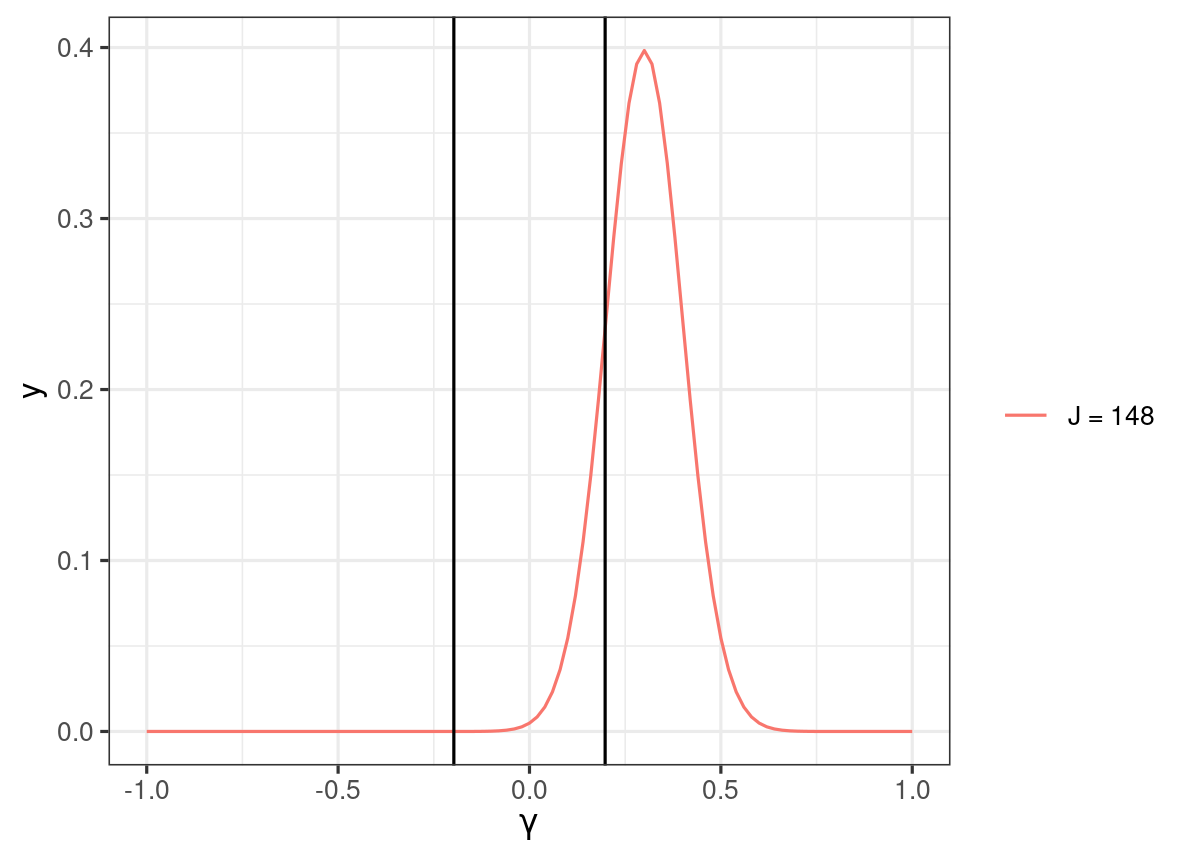
Power ≈P(^γ01≤−0.2)+P(^γ01≥0.2)=0.8461551
Tools for Power Analysis
Stand-alone programs
R packages
simr
Spreadsheet/Webapp
See more discussion in Arend & Schäfer (2019)
Monte Carlo Simulation for Power Analysis
Simulate a large number (e.g., R = 1,000) of data sets based on given effect size, ICC, etc
Fit an MLM to each simulated data
Power ≈ Proportion of times p<α
See sample R code for using simr
Uncertainty in Parameter Values
Uncertainty in Parameter Values
In the PowerUpR demo, to calculate the number of clusters J need to achieve 80% power, we determined
- Type I error rate = .05
- Two tailed test = TRUE
g2,r21,r22= 0, as we did not include any covariatesp= .5, for a balanced design (half treatment, half control)
However, we need to guess the values of
- Effect size = .3?
- ICC = .3?
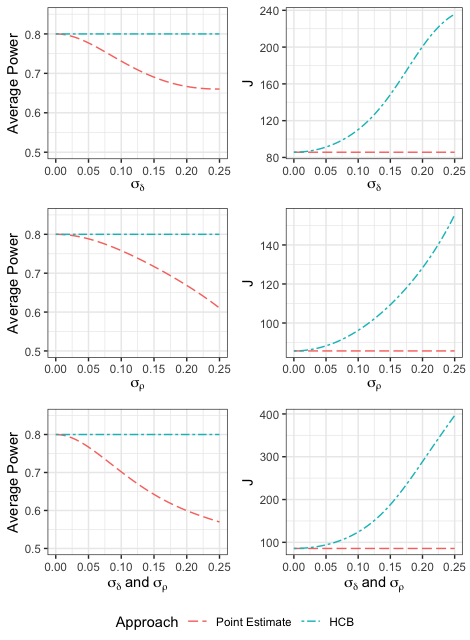
The Effect of Uncertainty in Power
Ignoring uncertainty
The more uncertainty we have but ignore about a parameter value, the more power loss we will have in our study (red curve)
Uncertainty in both effect size and ICC can further reduce our power
The more uncertainty we have, the more samples we need to achieve 80% power
Hybrid Classical-Bayesian approach
Incorporates uncertainty for sample size planning
Instead of plugging in a point value of a guess, we can specify how much uncertainty we have (e.g., standard error of γ01 from a previous study)
δ∼N(.3,.1)ρ∼Beta(a,b)
- where a, b can be calculated by ^ρ=.3 and σρ=.1 (estimate and uncertainty about ρ)

Additional Notes on Power
Increasing J usually leads to higher power than increasing n
Balanced designs generally have higher power than unbalanced designs
Larger sample size required for testing level-2 predictors
Testing an interaction requires a much larger sample size
- E.g., 16 times larger than for a main effect
Doubling J is better than doubling n