Review of Regression AnalysisPSYC 575Mark LaiUniversity of Southern California2020/08/04 (updated: 2021-08-29)1 / 18

Statistical Model

2 / 18

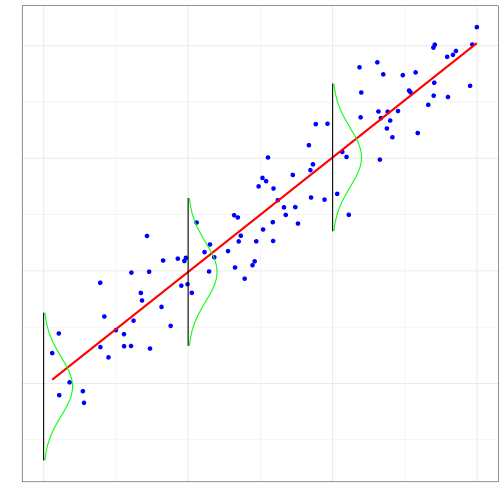
Statistical Model

A set of statistical assumptions describing how data are generated

Deterministic/fixed component

$Y_{i} = β_{0} + β_{1} X_{1 i} + β_{2} X_{2 i} + \dots$

Stochastic/random component

$Y_{i} = β_{0} + β_{1} X_{1 i} + β_{2} X_{2 i} + \dots + e_{i}$ $e_{i} \sim N (0, σ)$

2 / 18

It's only a review so I won't go deep.
You may check out the sections in the book by Gelman et al.
Model in OpenBoard
Statistical notation
- Notation for normal distribution
- Important for MLM

Why Regression?3 / 18

Why Regression?MLM is an extension of multiple regression to deal with data from multiple levels3 / 18

Learning ObjectivesRefresh your memory on regression4 / 18

Learning ObjectivesRefresh your memory on regressionDescribe the statistical model
4 / 18

Learning Objectives

Refresh your memory on regression

Describe the statistical model
Write out the model equations

4 / 18

Learning Objectives

Refresh your memory on regression

Describe the statistical model
Write out the model equations
Simulate data based on a regression model

4 / 18

Learning Objectives

Refresh your memory on regression

Describe the statistical model
Write out the model equations
Simulate data based on a regression model
Plot interactions

4 / 18

R Demonstration5 / 18

Transition to RStudio

Data Import
Explain the variables

Salary Data

From Cohen, Cohen, West & Aiken (2003)

Examine factors related to annual salary of faculty in a university department

6 / 18

Salary Data

From Cohen, Cohen, West & Aiken (2003)

Examine factors related to annual salary of faculty in a university department

time = years after receiving degree
pub = # of publications
sex = gender (0 = male, 1 = female)
citation = # of citations
salary = annual salary

6 / 18

Data Exploration

7 / 18

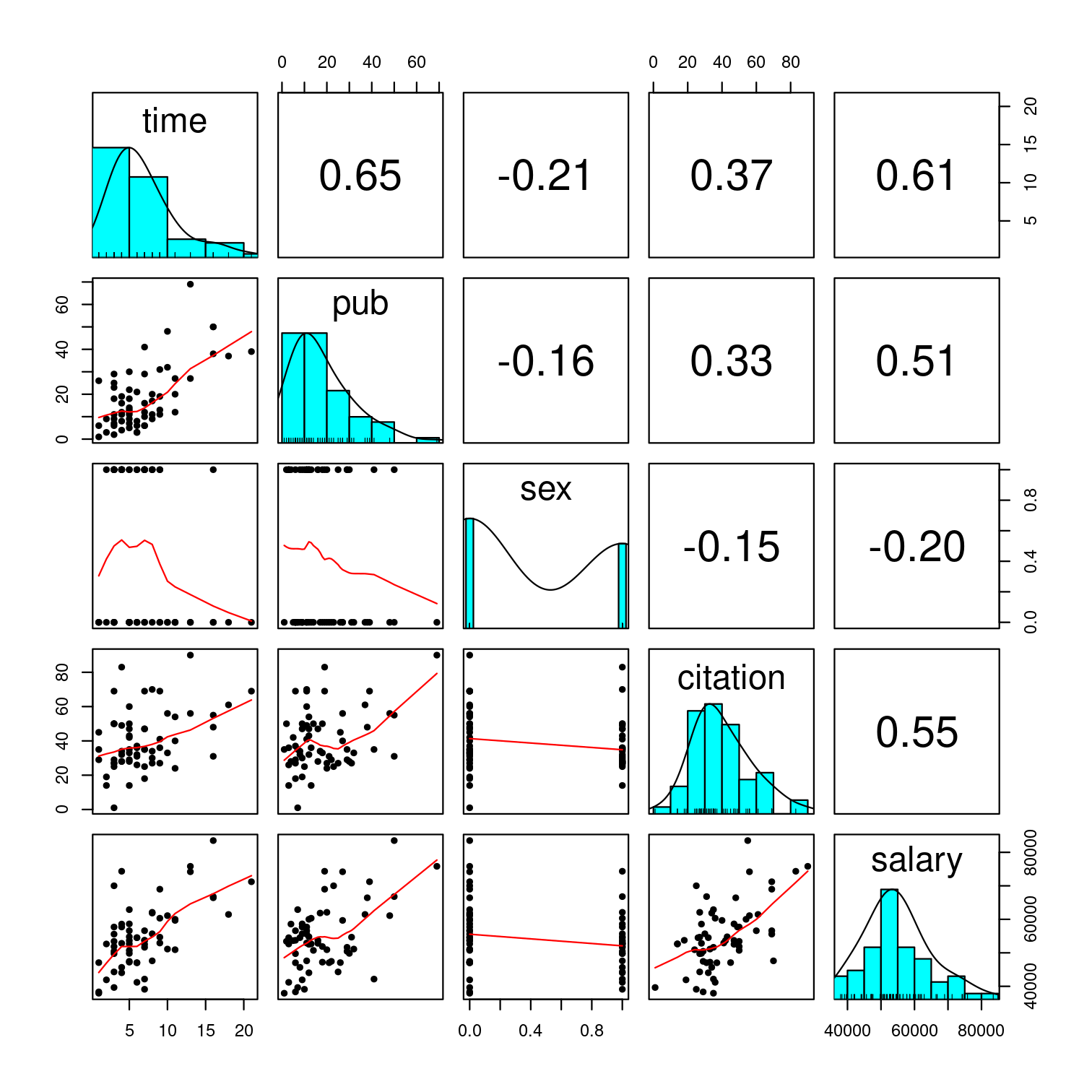
Explain what the x axis, y axis, diagonals are

Citation vs salary as an example

Data Exploration

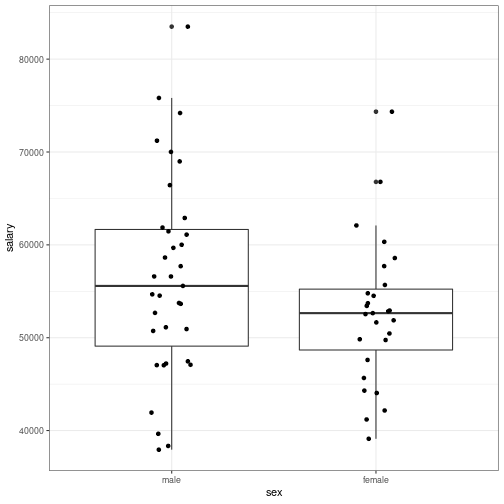
How does the distribution of salary look?
Are there more males or females in the data?
How would you describe the relationship between number of publications and salary?

7 / 18

Explain what the x axis, y axis, diagonals are

Citation vs salary as an example

Simple Linear RegressionSample regression lineConfidence intervalsCentering8 / 18

Regression line is only a sample estimate; there is uncertainty
Uncertainty measured by standard errors and confidence intervals
- Show animations on the varying regression slopes
- A function of sample size
Centering: Draw picture on changing the x-axis
Interpretations: unit increase in $x$ associated with $β$ unit increase in $y$

Simulation

See lecture and R code

9 / 18

Categorical Predictors

Dummy Coding

With $k$ categories, one needs $k - 1$ dummy variables

The coefficients are differences relative to the reference group

10 / 18

Categorical Predictors

Dummy Coding

With $k$ categories, one needs $k - 1$ dummy variables

The coefficients are differences relative to the reference group

10 / 18

Categorical Predictors

Dummy Coding

With $k$ categories, one needs $k - 1$ dummy variables

The coefficients are differences relative to the reference group

Male = 0

$y = β_{0} + β_{1} (0) = β_{0}$

11 / 18

Categorical Predictors

Dummy Coding

With $k$ categories, one needs $k - 1$ dummy variables

The coefficients are differences relative to the reference group

Male = 0

$y = β_{0} + β_{1} (0) = β_{0}$

Female = 1

$y = β_{0} + β_{1} (1) = β_{0} + β_{1}$

12 / 18

Multiple Regression13 / 18

Partial Effects

${salary}_{i} = β_{0} + β_{1} {pub}_{i}^{c} + β_{2} {time}_{i} + e_{i}$

14 / 18

Transition to R

Partial Effects

${salary}_{i} = β_{0} + β_{1} {pub}_{i}^{c} + β_{2} {time}_{i} + e_{i}$

Interpretations

Every unit increase in $X$ is associated with $β_{1}$ unit increase in $Y$ , when all other predictors are constant

14 / 18

Transition to R

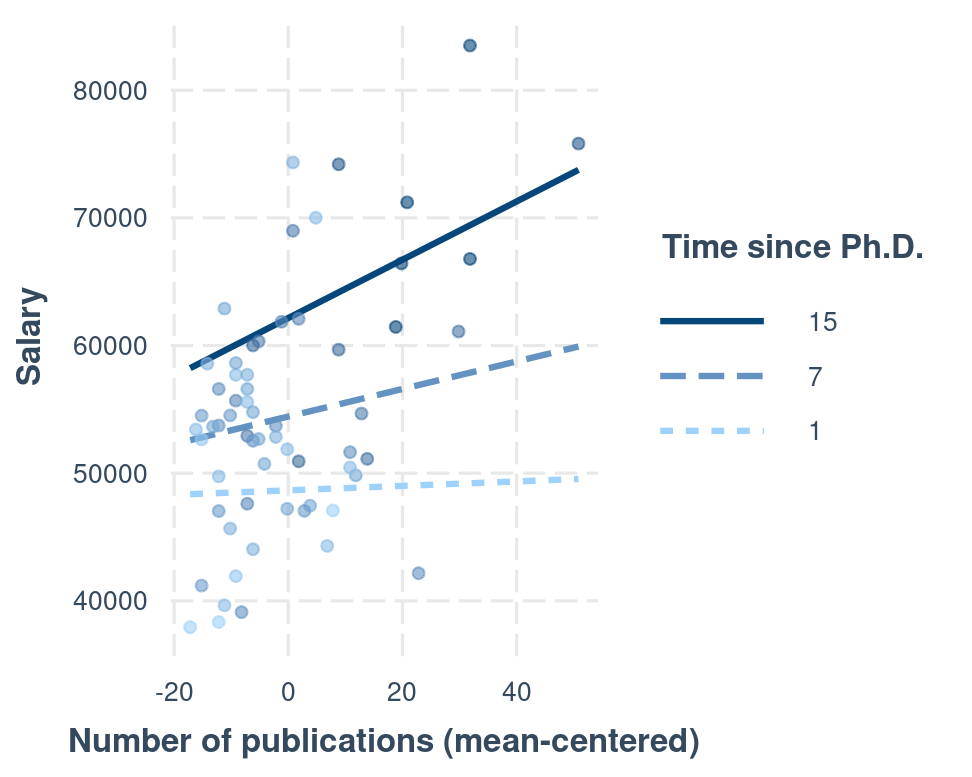
Interactions

Regression slope of a predictor depends on another predictor

$\begin{aligned} \hat{salary} & = 54238 + 105 \times {pub}^{c} + 964 \times {time}^{c} \\ + 15 ({pub}^{c}) ({time}^{c}) \end{aligned}$

15 / 18

Interactions

Regression slope of a predictor depends on another predictor

$\begin{aligned} \hat{salary} & = 54238 + 105 \times {pub}^{c} + 964 \times {time}^{c} \\ + 15 ({pub}^{c}) ({time}^{c}) \end{aligned}$

time = 7 $\Rightarrow$ time_c = 0.21

$\begin{aligned} \hat{salary} & = 54238 + 105 \times {pub}^{c} + 964 (0.21) \\ + 15 ({pub}^{c}) (0.21) \\ = 54440 + 120 \times {pub}^{c} \end{aligned}$

15 / 18

Interactions

Regression slope of a predictor depends on another predictor

$\begin{aligned} \hat{salary} & = 54238 + 105 \times {pub}^{c} + 964 \times {time}^{c} \\ + 15 ({pub}^{c}) ({time}^{c}) \end{aligned}$

time = 7 $\Rightarrow$ time_c = 0.21

$\begin{aligned} \hat{salary} & = 54238 + 105 \times {pub}^{c} + 964 (0.21) \\ + 15 ({pub}^{c}) (0.21) \\ = 54440 + 120 \times {pub}^{c} \end{aligned}$

time = 15 $\Rightarrow$ time_c = 8.21

$\begin{aligned} \hat{salary} & = 54238 + 105 \times {pub}^{c} + 964 (8.21) \\ + 15 ({pub}^{c}) (8.21) \\ = 62152 + 228 \times {pub}^{c} \end{aligned}$

15 / 18

Interactions

Regression slope of a predictor depends on another predictor

$\begin{aligned} \hat{salary} & = 54238 + 105 \times {pub}^{c} + 964 \times {time}^{c} \\ + 15 ({pub}^{c}) ({time}^{c}) \end{aligned}$

time = 7 $\Rightarrow$ time_c = 0.21

$\begin{aligned} \hat{salary} & = 54238 + 105 \times {pub}^{c} + 964 (0.21) \\ + 15 ({pub}^{c}) (0.21) \\ = 54440 + 120 \times {pub}^{c} \end{aligned}$

time = 15 $\Rightarrow$ time_c = 8.21

$\begin{aligned} \hat{salary} & = 54238 + 105 \times {pub}^{c} + 964 (8.21) \\ + 15 ({pub}^{c}) (8.21) \\ = 62152 + 228 \times {pub}^{c} \end{aligned}$

16 / 18

modelsummary::msummary()library(modelsummary)
msummary(list("M3 + Interaction" = m4),
         fmt = "%.1f")  # keep one digit

    M3 + Interaction 
  
    (Intercept) 
    54238.1 
  
    (1183.0) 
  
    pub_c 
    104.7 
  
    (98.4) 
  
    time_c 
    964.2 
  
    (339.7) 
  
    pub_c × time_c 
    15.1 
  
    (17.3) 
  
    Num.Obs. 
    62 
  
    R2 
    0.399 
  
    R2 Adj. 
    0.368 
  
    AIC 
    1291.8 
  
    BIC 
    1302.4 
  
    Log.Lik. 
    −640.895 
  
    F 
    12.817 
  
17 / 18

	M3 + Interaction
(Intercept)	54238.1
	(1183.0)
pub_c	104.7
	(98.4)
time_c	964.2
	(339.7)
pub_c × time_c	15.1
	(17.3)
Num.Obs.	62
R2	0.399
R2 Adj.	0.368
AIC	1291.8
BIC	1302.4
Log.Lik.	−640.895
F	12.817

Summary

Concepts

What is a statistical model
Linear/Multiple Regression
- Centering
- Categorical predictor
- Interpretations
- Interactions

HW 2

Try replicating the examples in the Rmd file

18 / 18

Help

Keyboard shortcuts

↑, ←, Pg Up, k

Go to previous slide

↓, →, Pg Dn, Space, j

Go to next slide

Home

Go to first slide

End

Go to last slide

Number + Return

Go to specific slide

b / m / f

Toggle blackout / mirrored / fullscreen mode

Clone slideshow

Toggle presenter mode

Restart the presentation timer

?, h

Toggle this help

Review of Regression Analysis

PSYC 575

Mark Lai

University of Southern California

2020/08/04 (updated: 2021-08-29)

Statistical Model

Statistical Model

A set of statistical assumptions describing how data are generated

Why Regression?

Why Regression?

MLM is an extension of multiple regression to deal with data from multiple levels

Learning Objectives

Refresh your memory on regression

Learning Objectives

Refresh your memory on regression

Learning Objectives

Refresh your memory on regression

Learning Objectives

Refresh your memory on regression

Learning Objectives

Refresh your memory on regression

R Demonstration

Salary Data

Salary Data

Data Exploration

Data Exploration

Simple Linear Regression

Sample regression line

Confidence intervals

Centering

Simulation

Categorical Predictors

Dummy Coding

Categorical Predictors

Dummy Coding

Categorical Predictors

Dummy Coding

Categorical Predictors

Dummy Coding

Multiple Regression

Partial Effects

Partial Effects

Interpretations

Every unit increase in XX is associated with β1β1 unit increase in YY, when all other predictors are constant

Interactions

Regression slope of a predictor depends on another predictor

Interactions

Regression slope of a predictor depends on another predictor

Interactions

Regression slope of a predictor depends on another predictor

Interactions

Regression slope of a predictor depends on another predictor

modelsummary::msummary()

Summary

Concepts

HW 2

Try replicating the examples in the Rmd file

Statistical Model

Help

Every unit increase in $X$ is associated with $β_{1}$ unit increase in $Y$ , when all other predictors are constant

`modelsummary::msummary()`